Hola a todos, hoy vamos a continuar con los ejercicios del libro: Evaluación Económica de Inversiones, del Doctor Rodrigo Varela. Continuemos entonces con el problema 5.11 (Alternativas que producen diferente servicio) :
5.11 Como gerente general de una organización que tiene cuatro plantas, Adolfo ha recibido una serie de propuestas de inversión para dichas plantas, caracterizada cada una por diferentes inversiones e ingresos. Las plantas se identifican con las letras K, N, X , W, y los proyectos de cada planta con números.
Si la tasa mínima de la organización es 26% anual, qué proyectos debe realizar Adolfo si:
a) Los proyectos de cada planta son mutuamente excluyentes, las plantas son independientes y disponen del siguiente dinero: 1) Ilimitado; 2) $3.000.000; 3) $1.800.000 y 4) $1.400.000
b) Los proyectos de cada planta son independientes, las plantas son independientes y disponen del siguiente dinero: 1) Ilimitado; 2) $3.000.000; 3) $1.800.000 y 4) $1.400.000
c) Todos los proyectos de todas las plantas son mutuamente excluyentes.
d) Las partidas presupuestales para cada planta son $1.000.000 y los proyectos de cada planta son mutuamente excluyentes.
e) Las partidas presupuestales para cada planta son $1.000.000 y los proyectos de cada planta son independientes.
Para responder las preguntas planteadas vamos a construir el siguiente modelo financiero en excel:
Teniendo calculado el VPN de cada proyecto, vamos a iniciar a responder las preguntas:
a) Como los proyectos son mutuamente excluyentes, Adolfo deberá elegir para cada planta el proyecto que tengan el VPN máximo, cuidando de que su selección no sobrepase el presupuesto disponible en los 4 escenarios:
1) Ilimitado: K4, N3, X2 y W2.
2) $3.000.000: K4, N3; X2 y W2.
3) $1.800.000: Para empezar a responder estos casos, vamos a incluir en el modelo la herramienta solver, para crear un modelo de programación lineal (ocultamos las columnas de los flujos C:L). Antes de trabajar con el Solver, hacemos los siguientes ajustes al modelo:
Que tiene la siguiente formulación:
Y a continuación, creamos el siguiente modelo de programación lineal:
Y dando clic en Resolver tenemos:
Entonces, Adolfo deberá elegir los proyectos: K4, X2 y W2. Note que en este momento, el modelo de programación podría llegar a permitir que se seleccionen dos proyectos en una misma planta.
4) $1.400.000: Volvemos a ejecutar el modelo con la nueva restricción:
Entonces, Adolfo deberá elegir realizar los proyectos X2 y W2.
b) Como los proyectos son independientes, Adolfo deberá elegir para cada planta los que tengan el VPN máximo, cuidando de que estos no sobrepasen el presupuesto disponible en cada escenario:
1) Ilimitado, vamos a asignar al modelo un valor de 6.760.000 que es lo que valen todos los proyectos y corremos el modelo:
Entonces, Adolfo deberá elegir los proyectos: K2, K4, N3, X2, W1, W2 y W3.
2) $3.000.000, actualizamos y corremos el modelo con la nueva restricción:
Donde podemos ver que Adolfo deberá elegir los proyectos: K4, N3, X2, W2 y W3.
3) $1.800.000, actualizamos y corremos el modelo con la nueva restricción:
Adolfo deberá elegir los proyectos: K4, X2 y W2.
4) $1.400.000, actualizamos y corremos el modelo con la nueva restricción:
Con esta restricción presupuestal, Adolfo deberá seleccionar los proyectos: X2 y W2.
c) En este caso, como todos los proyectos de todas las plantas son mutuamente excluyentes, Adolfo deberá elegir entre los 13 proyectos el que tenga el mayor VPN: X2, VPN $183.386.
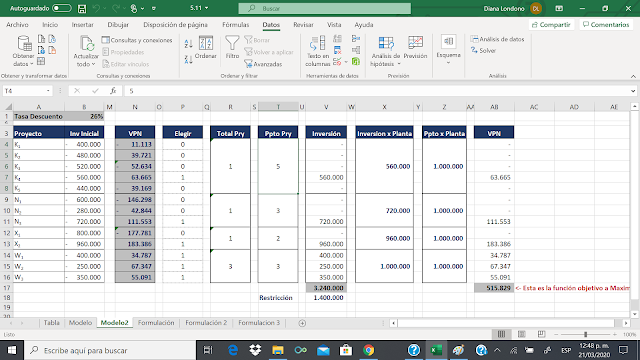
d) Para poder responder este punto, vamos a ajustar nuestro modelo como sigue:
Con la siguiente formulación:
Con estos ajustes, ahora podemos modelar presupuestos por planta y si son o no mutuamente excluyentes ( cantidad de proyectos por planta).
A continuación, incluimos en nuestro Solver las nuevas restricciones:
Y ejecutamos el modelo (antes de ejecutarlo, es importante que retiremos la restricción de la inversión total:
Entonces, dando clic en resolver tenemos:
Que con las nuevas restricciones, Adolfo deberá elegir los proyectos: K4, N3, X2 y W2.
e) Por último, vamos a actualizar nuestro modelo para responder este punto. Para esto, vamos a incluir la cantidad total de proyectos de cada planta en la columna T y ejecutamos nuevamente Solver:
Con lo que podemos concluir, que Adolfo deberá escoger los proyectos K4, N3, X2, W1, W2 y W3.
Hasta la próxima.
1) Ilimitado, vamos a asignar al modelo un valor de 6.760.000 que es lo que valen todos los proyectos y corremos el modelo:
Entonces, Adolfo deberá elegir los proyectos: K2, K4, N3, X2, W1, W2 y W3.
2) $3.000.000, actualizamos y corremos el modelo con la nueva restricción:
Donde podemos ver que Adolfo deberá elegir los proyectos: K4, N3, X2, W2 y W3.
3) $1.800.000, actualizamos y corremos el modelo con la nueva restricción:
Adolfo deberá elegir los proyectos: K4, X2 y W2.
4) $1.400.000, actualizamos y corremos el modelo con la nueva restricción:
Con esta restricción presupuestal, Adolfo deberá seleccionar los proyectos: X2 y W2.
c) En este caso, como todos los proyectos de todas las plantas son mutuamente excluyentes, Adolfo deberá elegir entre los 13 proyectos el que tenga el mayor VPN: X2, VPN $183.386.
d) Para poder responder este punto, vamos a ajustar nuestro modelo como sigue:
Con la siguiente formulación:
Con estos ajustes, ahora podemos modelar presupuestos por planta y si son o no mutuamente excluyentes ( cantidad de proyectos por planta).
A continuación, incluimos en nuestro Solver las nuevas restricciones:
Y ejecutamos el modelo (antes de ejecutarlo, es importante que retiremos la restricción de la inversión total:
Que con las nuevas restricciones, Adolfo deberá elegir los proyectos: K4, N3, X2 y W2.
e) Por último, vamos a actualizar nuestro modelo para responder este punto. Para esto, vamos a incluir la cantidad total de proyectos de cada planta en la columna T y ejecutamos nuevamente Solver:
Con lo que podemos concluir, que Adolfo deberá escoger los proyectos K4, N3, X2, W1, W2 y W3.
Hasta la próxima.



















No hay comentarios.:
Publicar un comentario