Matemática Financiera: Ejercicios 5.2, Problema 30 - Ahorro Quincenal Durante la Carrera Profesional - José Luis Villalobos

Hola a todos, hoy vamos a continuar con los ejercicios del libro: Matemáticas Financieras Tercera  Edición del autor José Luis Villalobos. 

Vamos a trabajar el problema 30 y lo resolveremos en excel y python:

30. ¿Para ayudar con los gastos de su graduación, una pareja de estudiantes decide depositar $450 cada quincena, desde que comienzan su carrera profesional. ¿Cuánto acumulan si el primer año ganan el 8.4% de interés anual capitalizable por quincenas, los siguientes dos les bonifican el 9.12% y los últimos 3 semestres, el 9.60% nominal quincenal?

Para resolver el problema, vamos a ayudarnos de un esquema gráfico que nos permita separar cada uno de los bloques de capitalización de acuerdo a las tasas que se van a reconocer a la pareja en cada momento de tiempo:

Estudiemos primero que ocurre con los 24 pagos que se realizan durante el primer año. Estos, se capitalizan con una tasa del 8.40%, pero finalizadas las 24 quincenas, el valor que se ha acumulado en la cuenta donde se están depositando dichos pagos se continuará capitalizando, y para los próximos dos años la tasa con la que lo hará es del 9.12%. Pasados los dos años (o 48 quincenas), el valor que tenemos acumulado se empezará a incrementar hasta el final del plan de ahorro a una tasa del 9.60%.

Los 48 pagos quincenales que se realizan entre el año 2 y el 3 tienen primero una capitalización del 9.12% y el valor que se acumula en la cuenta por dichos pagos, pasa a tener una capitalización del 9.60% hasta el final de la carrera.

Por último, los pagos entre el año 4 y 5 (36 quincenas) solamente se capitalizan por el 9.60% hasta terminar los estudios.

Al hacer esta división del problema por bloques, podemos entenderlo más fácilmente que si lo abordáramos como un todo.

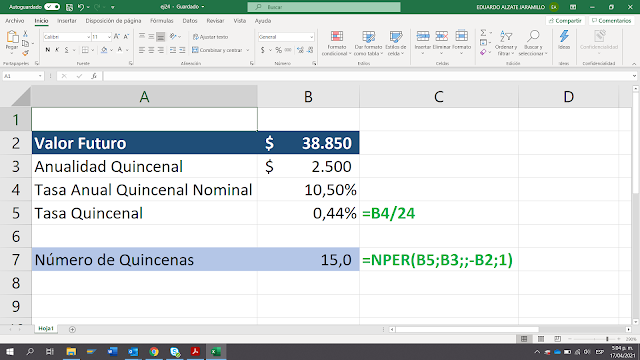
Los párrafos anteriores, los podemos formular en excel de la siguiente manera (seguiremos asumiendo que los pagos ocurren al inicio de cada periodo):

Como se puede ver en el excel, los primeros 24 pagos quincenales del año 1 tienen 3 momentos de capitalización con 3 tasas diferentes. Los 48 pagos que se dan en el año 2 y 3m tienen dos momentos con dos tasa y por último los del año 4 en adelante tienen una sola tasa.

Matemática Financiera: Ejercicios 5.2, Problema 29 - Número de Periodos para Alcanzar un Valor Futuro - José Luis Villalobos

Hola a todos, hoy vamos a continuar con los ejercicios del libro: Matemáticas Financieras Tercera  Edición del autor José Luis Villalobos. 

Vamos a trabajar el problema 29 y lo resolveremos en excel y python:

29. ¿Cuántos pagos bimestrales de $8,193, se necesitan para alcanzar un monto de $70,000, si se devengan intereses del 8.76% capitalizable por bimestre?

Para resolver el problema, vamos a construir el siguiente modelo financiero en excel (vamos a asumir el pago de las anualidades al comienzo de cada período):

Utilizando la función NPER() de excel, podemos establecer el número de bimestres necesarios para alcanzar los $70,000 en el futuro, en este caso, se requieren 8 bimestres.

Para resolver el problema en python, vamos a escribir el siguiente script en la plataforma google-colab:

Al ejecutar nuestro script, llegamos al mismo resultado que obtuvimos previamente en excel.

A continuación el código fuente:

Matemática Financiera: Ejercicios 5.2, Problema 28 - Valor Inicial de Inversión más Anualidad - José Luis Villalobos

Hola a todos, hoy vamos a continuar con los ejercicios del libro: Matemáticas Financieras Tercera  Edición del autor José Luis Villalobos. 

Vamos a trabajar el problema 28 y lo resolveremos en excel y python:

28. ¿Un estudiante abre una cuenta en un banco que paga el 15.6% nominal quincenal y continúa depositando $1,750 cada quincena al inicio. 20 meses después de que la abrió tiene acumulados $90,857.45. ¿Con cuánto inició sus ahorros?

Para resolver el problema, vamos a construir el siguiente modelo financiero en excel (vamos a asumir el pago de las anualidades al comienzo de cada período):

Utilizando la función VA() de excel, vamos a calcular el monto inicial con el que se abrió la cuenta. Como podemos ver, la cuenta fue abierta con $8,250.

Para resolver en python, vamos a escribir el siguiente script en la plataforma colab de google:

Como pueden ver, con el script llegamos al mismo valor que obtuvimos previamente en excel.

A continuación el código fuente: 

Matemática Financiera: Ejercicios 5.2, Problema 26 - Valor de una Anualidad para Librar un Pagaré - José Luis Villalobos

Hola a todos, hoy vamos a continuar con los ejercicios del libro: Matemáticas Financieras Tercera  Edición del autor José Luis Villalobos. 

Vamos a trabajar el problema 26 y lo resolveremos en excel y python:

26. ¿El matemático González firma un documento por un crédito de $32,570, con cargos del 13% simple anual y plazo de 6 meses. ¿Cuánto debe depositar cada semana en una cuenta que bonifica el 11.44% nominal semanal para librar el pagaré? Suponga que abre la cuenta cuando firma el documento.?

Para resolver el problema, vamos a construir el siguiente modelo financiero en excel (vamos a asumir el pago de las anualidades al comienzo de cada período):

Como se puede ver en el modelo, necesitamos hacer dos cálculos. El primero, para determinar el valor que tendrá el pagaré al final de los seis meses pactados por González. Como el documento se fijó con una tasa simple, calculamos los intereses dividiendo la tasa por dos y se la aplicamos al capital, con lo que llegamos al valor de $34,687,05.

El segundo cálculo, es para establecer las anualidades a depositar al comienzo de cada semana, para llegar al valor futuro que calculamos con anterioridad, solo que en este caso, la cuenta en la que lo vamos a hacer, reconoce intereses compuestos. Utilizando la función PAGO() de excel, establecemos que el valor de los 26 depósitos será de $1,294.94.

Asumimos que en un año hay 52 semanas y que en un semestre tenemos la mitad, es decir 26.

En el problema 27 nos preguntan: ¿Cuánto ganó o perdió por intereses el matemático?

En el documento de crédito pagamos: $34,687.05 - $32,570 = $2,117.05.

Y en la cuenta nos pagaron: ($1,294.94 x 26) - $34,687.05 = $1,018.53.

En el neto de las dos operaciones, nuestro matemático perdió: $2,117.05 - $1,018.53 = $1,098.52.

Ahora vamos a resolver el problema en python, escribiendo el siguiente script:

Con lo que llegamos al mismo resultado que obtuvimos previamente en excel.

A continuación el código fuente:

Matemática Financiera: Ejercicios 5.2, Problema 24 - Número de períodos para alcanzar un valor futuro - José Luis Villalobos

Hola a todos, hoy vamos a continuar con los ejercicios del libro: Matemáticas Financieras Tercera  Edición del autor José Luis Villalobos. 

Vamos a trabajar el problema 24 y lo resolveremos en excel y python:

24. ¿En cuánto tiempo se acumulan $38,850, depositando $2,500 cada quincena al 10.5% nominal quincenal?

Para resolver el problema, vamos a construir el siguiente modelo financiero en excel (vamos a asumir el pago de las anualidades al comienzo de cada período):

Utilizando la función NPER() de excel, vamos a calcular el número de períodos necesarios para acumular $38,850 con las condiciones planteadas en el ejercicio. Como podemos ver, vamos a necesitar de 15 quincenas para poder acumular dicha cantidad.

En el problema 25, nos preguntan ¿Cuánto se devenga por intereses en el problema 24? Para dar respuesta realizamos la siguiente operación:

intereses = $38,500 - ($2,500 x 15) = $1,350.

Para resolver en python, vamos a escribir el siguiente script en la plataforma colab de google:

Y cuando lo ejecutamos, llegamos al mismo resultado que obtuvimos previamente en excel:

A continuación el código fuente:

Matemática Financiera: Ejercicios 5.2, Problema 23 - Pagos uniformes necesarios para alcanzar un valor futuro - José Luis Villalobos

Hola a todos, hoy vamos a continuar con los ejercicios del libro: Matemáticas Financieras Tercera  Edición del autor José Luis Villalobos. 

Vamos a trabajar el problema 23 y lo resolveremos en excel y python:

23. ¿Cuánto debe invertirse cada mes al 13.8% capitalizable por meses, para disponer de $129,000 en un año?

Para resolver el problema vamos a construir el siguiente modelo financiero en excel (vamos a asumir el pago de cada anualidad al inicio de los periodos):

Utilizando la función PAGO() de excel, encontramos que el monto de las anualidades uniformes con las que lograremos acumular $129,000 en 12 meses es de $9,972.22.

Para resolver el problema en python vamos a escribir el siguiente script en la plataforma colab:

Como podemos ver, utilizando la función pmt del paquete numpy_financial llegamos al mismo resultado: anualidades de $9,972.22.

A continuación el código fuente:

Matemática Financiera: Ejercicios 5.2, Problema 22 - Valor futuro de una anualidad - José Luis Villalobos

Hola a todos, hoy vamos a continuar con los ejercicios del libro: Matemáticas Financieras Tercera  Edición del autor José Luis Villalobos. 

Vamos a trabajar el problema 22 y lo resolveremos en excel y python:

22. ¿Cuánto se acumula con 13 depósitos semanales de $1,750 en una cuenta que bonifica intereses del 9.10% anual capitalizable por semanas?

Para resolver el ejercicio, vamos a construir el siguiente modelo financiero en excel:

Utilizando la función VF() de excel, calculamos el valor futuro de las 13 anualidades. Para este ejercicio, vamos a suponer que los depósitos se realizan al inicio de cada semana. Como pueden ver, el valor que se va a acumular en la cuenta, al final de los 13 depósitos es de $23,030.65.

Ahora, vamos a resolver el ejercicio en Python, para esto utilizamos nuestra plataforma colab:

Con lo que llegamos al mismo resultado.

A continuación el código fuente: