Matemática Financiera: Cuotas Financiación Compra Vehículo. Problema 2.10 - Evaluación Económica de Inversiones. Rodrigo Varela

Hola, hoy vamos a resolver el problema 2.10 del libro: Evaluación Económica de Inversiones.

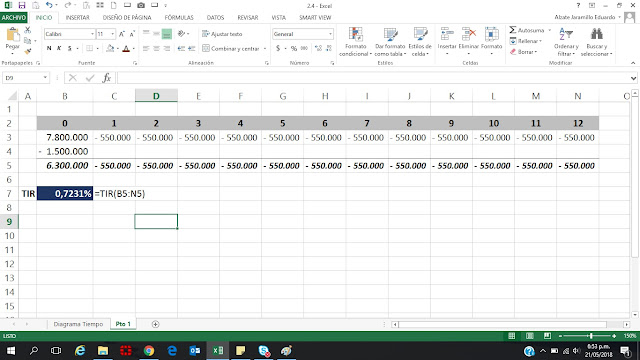
2.10 Si Jorge compra un auto por $4.500.000 y da $2.000.000 como cuota inicial, ¿Qué cuotas mensuales debe pagar al final de los 30 meses siguientes, para cubrir la cantidad financiada, si el interés es el 24% anual compuesto mensualmente? ¿Cuál sería su cuota si el interés fuese el 24% anual?

Vamos a construir el siguiente modelo en Excel con el que vamos a dar respuesta a los dos interrogantes:

En el Punto 1, tenemos que el interés del 24% es de tipo nominal, entonces, para llevarlo a mensual, solo tenemos que dividirlo entre 12 (como se ve en la fórmula de la celda C8). Teniendo el interés mensual, solo necesitamos aplicar la función PAGO() y listo, la respuesta es que para financiar $2.500.000 a 30 meses con un interés del 2% mensual, se deben cancelar cuotas mensuales de $111.624,81.

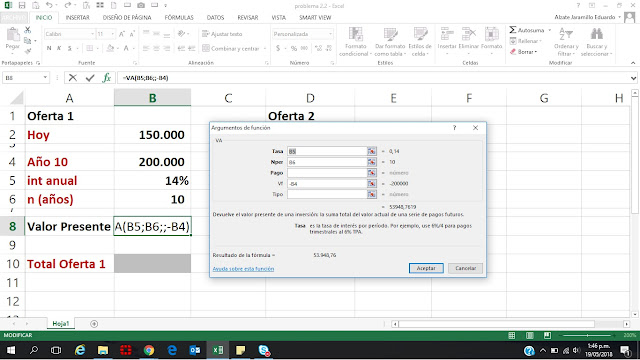
En el Punto 2, tenemos que el interés del 24% es de tipo efectivo, entonces, para llevarlo a mensual, debemos utilizar la fórmula de la celda G8 (también podemos hacerlo como se ve en este enlace: Calcular la tasa mensual equivalente a partir de la efectiva anual utilizando la función: TASA.NOMINAL( )).

Teniendo el interés mensual, solo necesitamos aplicar la función PAGO() y listo, la respuesta es que para financiar $2.500.000 a 30 meses con un interés del 1,8% mensual, se deben cancelar cuotas mensuales de $108.710,99.

Hasta una próxima.

Matemática Financiera: Resultado de Inversión - Capitalización Anual y Mensual. Problema 2.9 - Evaluación Económica de Inversiones. Rodrigo Varela

Hola, hoy vamos a resolver el problema 2.9 del libro: Evaluación Económica de Inversiones.

2.9 ¿Cuánto se acumulará al final de 10 años si hoy invierto $200.000 y dentro de 5 años invierto $150.000, con un interés del 18% anual? ¿Cuánto sería el resultado si el interés fuese el 18% anual compuesto mensualmente?

Veamos el diagrama de tiempo:

Para resolver el problema, lo que tenemos que hacer es llevar los dos pagos a valor futuro (10 años). Modelamos en Excel:

Que en 10 años, nuestra inversión tendrá un valor de $1.389.930,77. Como pueden ver, lo que hicimos fue encontrar el valor futuro de los $200.000 dentro de 10 años y el de los $150.000 dentro de cinco. Ambos, incrementados en un 18% anual.

Matemática Financiera: Gradiente - Repartición de Herencia. Problema 2.8 - Evaluación Económica de Inversiones. Rodrigo Varela

Hola a todos, continuando con el desarrollo de los problemas del libro: Evaluación Económica de Inversiones. Hoy vamos a trabajar el problema 2.8 que consiste en una inversión con un retorno del tipo gradiente:

2.8 La herencia del señor Rico asciende a $1.000.000, depositados en un fondo que produce el 18% anual. El señor Rico dispone en su testamento que el primer año se entreguen a sus herederos $200.000, el segundo año $210.000, el tercero $220.000, etc. ¿Durante cuántos años se pueden hacer los pagos? (La respuesta puede ser decimal).¿Cuántos años habría durado si el esquema hubiese sido $250.000, $240.000, $230.000, etc.¿Cuánto si hubiesen sido pagos uniformes de $220.000? ¿Cuánto si hubiesen sido pagos uniformes de $180.000? Discuta los resultados.

Este problema es diferente a una anualidad uniforme, dado que el valor del pago mensual se incrementa de forma constante frente al pago del periodo anterior. En este problema, el factor por el que se incrementa es $10.000.

Para resolver el problema, vamos a dar una solución por un método intuitivo con el objetivo de dar respuesta al primer y segundo interrogante. Para esto, vamos a modelar 11 pagos y les vamos a calcular el valor presente:

Como se ve en la imagen, en la columna E tenemos el cálculo del valor presente neto de los pagos que se realizan según van pasando los años. Por ejemplo, en el tercer año se completarán 3 pagos, en el año 1: $200.000, año 2: $210.000 y año 3: $220.000. 

Estos tres pagos que suman $630.000 (dejando de lado el concepto del valor del dinero en el tiempo), cuando se descuentan a una tasa del 18% anula, equivalen a $454.209 (columna E) de hoy. Entonces, para dar respuesta a la pregunta realizada, debemos identificar en que año, el valor presente no es superior a $1.000.000:

Matemática Financiera: Valor Mina de Azufre Parte 2. Problema 2.7 - Evaluación Económica de Inversiones. Rodrigo Varela

Hola a todos, continuando con el desarrollo de los problemas del libro: Evaluación Económica de Inversiones. Hoy vamos a trabajar el problema 2.7, que en últimas es una extensión del problema 2.6 sobre la valoración de la mina de azufre:

2.7* ¿Cuál sería la utilidad/ton del problema anterior en caso de ser uniforme, para que llegue a ser equivalente a las utilidades diferenciales?

En este problema, lo que nos piden es hallar una utilidad por tonelada que sea igual en todos los años y que al descontar la utilidad a una tasa del 16% lleguemos a los mismos $6.558.242,89 del problema anterior. Este, sin duda, es un trabajo para nuestro apreciado amigo Solver.

Vamos entonces a iniciar extendiendo el modelo anterior incluyendo una utilidad/ton uniforme:

En este modelo, iniciamos definiendo una utilidad por tonelada de $1. La celda I2 sombreada en amarillo es la celda que vamos a poner a variar y todas las otras utilidades por tonelada de la columna I son iguales a ella. Lo podemos ver activando el rastreo de celdas dependientes:

Matemática Financiera: Valor Mina de Azufre. Problema 2.6 - Evaluación Económica de Inversiones. Rodrigo Varela

Hola a todos, continuando con el desarrollo de los problemas del libro: Evaluación Económica de Inversiones. Hoy vamos a trabajar el problema 2.6:

2.6* Se estima que un depósito de azufre producirá 20.000 toneladas este año y que la producción disminuirá en 500 ton/año hasta el final del proyecto, el cual ocurrirá en 20 años. La utilidad neta será $60/ton durante los primeros 9 años y $80/ton durante los 11 años restantes. ¿En cuánto podemos valorar la mina, hoy día, si la tasa mínima de retorno es 16% anual?

Para este ejercicio no vamos a construir un diagrama de tiempo, vamos a modelar directamente en el Excel:

Modelamos los 20 periodos, disminuyendo en 500 las toneladas cada año y la utilidad por tonelada como esta planteado en el problema. La utilidad de cada periodo, es igual al producto entre las toneladas y la utilidad por tonelada (columna D).

Calculamos el valor presente de la utilidad en los 20 periodos utilizando la función VNA() de Excel:

Y listo, el valor de la mina de azufre, de acuerdo con los 20 flujos proyectados de utilidad es de $6.558.242,89.

Eso es todo. Hasta una próxima.

Matemática Financiera: Valor Nominal de Vehículo. Problema 2.5 - Evaluación Económica de Inversiones. Rodrigo Varela

Hola, hoy vamos a resolver el problema 2.5 del libro: Evaluación Económica de Inversiones.

2.5 Un señor compra un auto y deposita el 30% de su valor como cuota inicial; además, para pagar la diferencia, firma 24 letras con vencimiento mensual. El interés es del 1,5% mensual. Después de efectuar 14 pagos, le informan que las 10 letras restantes valen $350.000 si las paga inmediatamente. ¿Cuál era el valor nominal del vehículo?

Tenemos entonces nuestro diagrama de tiempo:

Para resolver el problema, entonces vamos a encontrar cuál es el valor de cada una de esas últimas 10 cuotas (pintadas en verde) descontadas al 1,5% y que equivalen a $350.000 de ese momento:

Utilizando la función PAGO(), tenemos que el valor de las cuotas era de $37.951,96.

Aplicando las 5S en Nuestra Oficina

Hola a todos. Hoy vamos a hacer una pausa en los posts de Matemáticas Financieras y vamos a tocar otro importante tema: El del Mejoramiento Continuo. Específicamente, desde el punto de vista de la metodología de las 5S.

Siempre ha existido una discusión sobre la aplicación de las 5S en las oficinas de Administración de una empresa. Hay muchas personas que creen con firmeza que esta metodología encuentra su mayor aplicación en las áreas operativas, en las plantas de empresas manufactureras, en talleres de ensamble etc. 

Creo que las 5S tienen una amplia aplicación en cualquier área, sin importar si es una empresa manufacturera, comercializadora o de servicios. Incluso, esta metodología la podemos aplicar en nuestras propias casas. Aquel cuarto que se ha convertido de un momento a otro en depósito de todo lo que no nos sirve, el cajón de nuestra mesa de noche, los gabinetes de la cocina etc.

Para los que les interese conocer un poco sobre la metodología, su definición y sus cinco piezas clave, aquí les dejo el enlace a wikipedia: https://es.wikipedia.org/wiki/5S

Sobre las 5 etapas o piezas de la metodología, sin duda, la de mayor desafío es la de mantener la disciplina. Es decir, una vez se han aplicado las otras 4, asegurarse que nuestro cajón, planta, cuarto etc no se conviertan de nuevo en colectores de cosas sin ningún orden.

Aunque lo pueden ver con más detalle en el enlace anterior, estos son los 5 componentes de las 5S:

La aplicación que vamos a ver a continuación, se realizó en una empresa de servicios a un mueble que servía de biblioteca, archivo temporal, lugar de almacenaje de los documentos que llegaban al área y hasta de otras cosas.

Matemática Financiera: Compra de Vehículo. Problema 2.4 - Evaluación Económica de Inversiones. Rodrigo Varela

Hola, hoy vamos a resolver el problema 2.4 del libro: Evaluación Económica de Inversiones.

2.4 Una organización que desea comprar un vehículo que cuesta $7.800.000, puede pagar $1.500.000 de contado y el resto en 12 meses. La financiera XW acepta 12 cuotas de $550.000 y la financiera XY ofrece financiar al 0,75% mensual. ¿Cuál financiación debe aceptar? ¿Qué interés mensual cobra la XW? ¿Cuáles serían las cuotas en la XY?

Al igual que en los ejercicios anteriores, vamos a iniciar con el diagrama de tiempo. En este problema, el diagrama a trabajar es el de la financiera XW:

Como pueden ver, en el periodo cero se recibe el vehículo por $7.800.000 (ingreso) y pagamos la cuota inicial por $1.500.000 (egreso) lo que nos da un flujo neto de $6.300.000. 

Lo modelamos en Excel y utilizamos la función para calcular la TIR (Celda B7):

Matemática Financiera: Análisis Prestamo. Problema 2.3 - Evaluación Económica de Inversiones. Rodrigo Varela

Hola, continuando con el desarrollo de los problemas del libro: Evaluación Económica de Inversiones. Hoy vamos a trabajar el problema 2.3:

2.3 La organización para la cual usted trabaja tiene un fondo de préstamos de emergencia, cuyo reglamento establece que los créditos serán  12 meses y que las cuotas 3, 6, 9 y 12 serán el doble de las demás. Asimismo, el interés es del 1,5% mensual. La cantidad que le van a prestar depende de la cuota.

Si le prestan $50.000, ¿cuáles serán sus cuotas normales?

Si sus cuotas normales son $10.000, ¿cuál sería el valor del préstamo?

De nuevo vamos a elaborar nuestro diagrama de tiempo:

Como pueden ver en el diagrama, el problema se puede interpretar como 12 cuotas mensuales A y 4 cuotas trimestrales A. El único cuidado que hay que tener es que la tasa 1,5% es mensual, entonces, para descontar las 4 cuotas trimestrales A, hay que convertir los 1,5% mensual a trimestral.

Vamos a resolver el primer punto de dos formas alternas. La primera es utilizando la función VNA() y la utilidad Solver de Excel. Vamos a crear un modelo como sigue:

Matemática Financiera: Decisión de Inversión. Problema 2.2 - Evaluación Económica de Inversiones. Rodrigo Varela

Vamos a continuar con el desarrollo de los problemas del libro: Evaluación Económica de Inversiones. Hoy vamos a trabajar el problema 2.2:

2.2 Un inversor recibe ofertas de dos compañías. Tiene que decidir cuál es la mejor oferta tomando como punto de referencia la posibilidad de invertir al 14% anual.

Oferta 1: $150.000 hoy y $200.000 dentro de 10 años.

Oferta 2: $30.000 al final de cada uno de los próximos 10 años.

Como siempre, vamos a iniciar por dibujar el diagrama de tiempo de las dos ofertas:

En el caso de la oferta uno, lo que tenemos es un valor de $150.000 que están en el periodo cero, al que no le tenemos que hacer ningún cálculo y $200.000 que están en el año 10. Estos últimos, los debemos descontar con la tasa del 14% anual para traerlos a valor presente y poder sumarlos a los $150.000. Vamos a hacerlo en Excel utilizando la función VA() (valor presente o valor actual):

Matemática Financiera: Amortización Préstamo. Problema 2.1 - Evaluación Económica de Inversiones. Rodrigo Varela

Hola a todos, después de un buen descanso, hoy estamos de vuelta en el blog. Vamos a empezar a trabajar temas más asociados con matemáticas financieras y finanzas en general, sin dejar de lado los temas de programación, SQL y SAP que tanto disfruto. 

Para los temas de matemáticas financieras, voy a trabajar los problemas de uno de los libros más completos que conózco: Evaluación Económica de Inversiones de Rodrigo Varela:

Todo el crédito de la propiedad intelectual de los problemas planteados para el Doctor Varela.

Iniciemos entonces con el problema 2.1 del libro:

2.1 Una firma financiera le ofrece un préstamo por $1.000.000 a 60 meses, con un interés mensual del 3%. Determine el valor de los pagos mensuales. ¿A cuánto ascenderían los pagos mensuales sí el interés fuese del 1,5% mensual?